Bár több ezer éve épült, az ókori mérnökök a matematika révén mégis elrejtettek benne egy rejtélyes törvényszerűséget. Legalább annyira rejtélyeset, mint amilyenek maguk a piramisok.
Az ördög az arányokban rejlik
A hivatalos nézőpont szerint az i. e. 26. században épült gízai nagy piramis mára az egyedüli fennmaradt építmény a világ hét csodája közül.
Az épületre vonatkozó terveket egy bizonyos Hemiunu herceg készítette el. Ő volt tehát az, aki végérvényesen az utókor tudtára adta: az ókori Egyiptomban már ismerték azt az arányosságot, amelyre ma ugyanúgy technikai mintázatok hosszú sora épül.
De ne rohanjunk annyira előre, bemelegítésként végezzünk el egy kis fejszámolást. Osszuk el a piramis alapélének a felét (átlag 115,18 m) oldallapjai magasságával (kb. 186,42 m). Na jó, a fejszámolással csak vicceltem.
Ha a számot 3 tizedesjegyre kerekítjük, 0,618-at kapunk. Első ránézésre semmi érdekes. Kivéve persze azoknak, akik valamivel jártasabbak a kereskedésben, őket azonban szeretném megkérni, hogy ne lőjék le a poént.
A matematika egyik legszebb arányosságáról van ugyanis szó, amely néhány sort még megérdemel: ez az aranymetszés.
Méltán nevezhetnénk egyfajta hídnak a matematika és a természet között. Számtanilag és geometriailag ugyanúgy meghatározható, mint ahogyan a körülöttünk lévő világban is fellelhető.

Az ember számára – valahol tudat alatt – ez számít a szimmetria egyik sarokkövének. Az emberi arcon, a testen, de a csigák mészvázán is számtalan ponton megtalálhatjuk ezt az arányt.
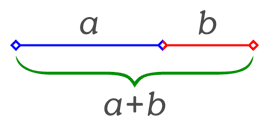
Többféle módon kiszámítható. Geometriailag: húzzunk egy szakaszt és osszuk fel egy rövidebb és egy hosszabb szakaszokra. Amennyiben a rövidebb szakasz úgy aránylik a hosszabbikhoz, mint a hosszabbik az eredetileg rajzolt teljes szakaszhoz, akkor gratulálok! Megtaláltad az aranyarányt.
Ha ebből a definícióból indulunk ki, levezethetjük az aranymetszés, vagyis a fí értékét: (√5+1)/2≈1,618… (kerekített érték!). Nem kell megijedni, csodálkozni kell: eggyel nagyobb számot kaptunk, mint a korábbi 0,618.
Az aranymetszésben ugyanis az is rendkívül érdekes, hogy amennyiben a reciprokát vizsgáljuk (vagyis 1/1,618), akkor 0,618-at kapunk, ti. 1-gyel kisebb számot. Mindez pedig visszafelé is működik.
Egy egyszerű, mégis rejtélyes számsor
A fít szintén megkaphatjuk az alábbi módon: írjunk fel egy olyan számsorozatot, amelyben minden tag (az első kettőt kivéve) az előtte lévő két tag összege: pl.: 0, 1, 1, 2, 3, 5, 8, 13… Ezt a sort természetesen a végtelenségig folytathatnánk.
Most válasszuk ki bármelyik tagot (lehetőleg minél nagyobbat), és osszuk el az előtte lévővel! Legyen mondjuk 13 / 8 = 1,625. Ajaj, kísértetiesen közel van. Menjünk feljebb! 21 / 13 = 1,6154…
Minél nagyobb számokkal dolgoznánk, annál jobban közelítenénk az aranymetszés értékéhez.
A két bekezdéssel korábban felírt számsorozatnak egyébként van egy megnevezése is: Fibonacci-számsornak hívjuk.
Ugyanazok a Fibonacci-számok, amelyekkel technikai elemzésekben szereplő támasz- és ellenállásszintek meghatározhatók. Ennek mögöttes módszerével már nem fárasztalak titeket.
Nem tudjuk, mi okozza
A mögöttes logika egyébként nem ismert. Én személy szerint lélektani okokat látok mögötte.
Az aranymetszés ugyanis – ahogy korábban említettem – egy nagyon komoly szimmetriával bír. Ezzel az aránnyal nem lehet mellényúlni. Ha mondjuk nem tudjuk eldönteni, hogy milyen magasra szereljük a házszámot vagy hová akasszunk fel egy képet a falra, egy kis számolgatás után az aranyaránnyal biztos nem tévedhetünk.
Ebből következhet az is, hogy amikor a kereskedő vet egy pillantást valamilyen csártra, elképzelhető, hogy valamiféle szimmetriai okból kifolyólag azon a ponton nyit üzletet.
Persze az sem kizárt, hogy amikor ezt a mérőszámot tesztelték, pont úgy alakult az ár, ahogyan számítottak rá, azóta pedig egyfajta önbeteljesítő jóslatként működik.